反悔贪心

穿梭时间的画面的钟 从反方向开始移动 回到当初爱你的时空

定义

反悔贪心有别于朴素贪心在于，我们通过“反悔”的操作用更后面的局部最优解去修正前面的局部最优解，从而得到全局最优解。本质上仍然符合贪心的局部最优=全局最优的定义，我们只是判断如果当前这一步不满足全局最优解，那就退回一步。

不加反悔的一直朝着当前局面的最优解走很可能导致我们被困在局部的最优解而无法到达全局的最优解，就好像我们爬山就只爬到了一座山的山顶却没有到整片山的最高处：

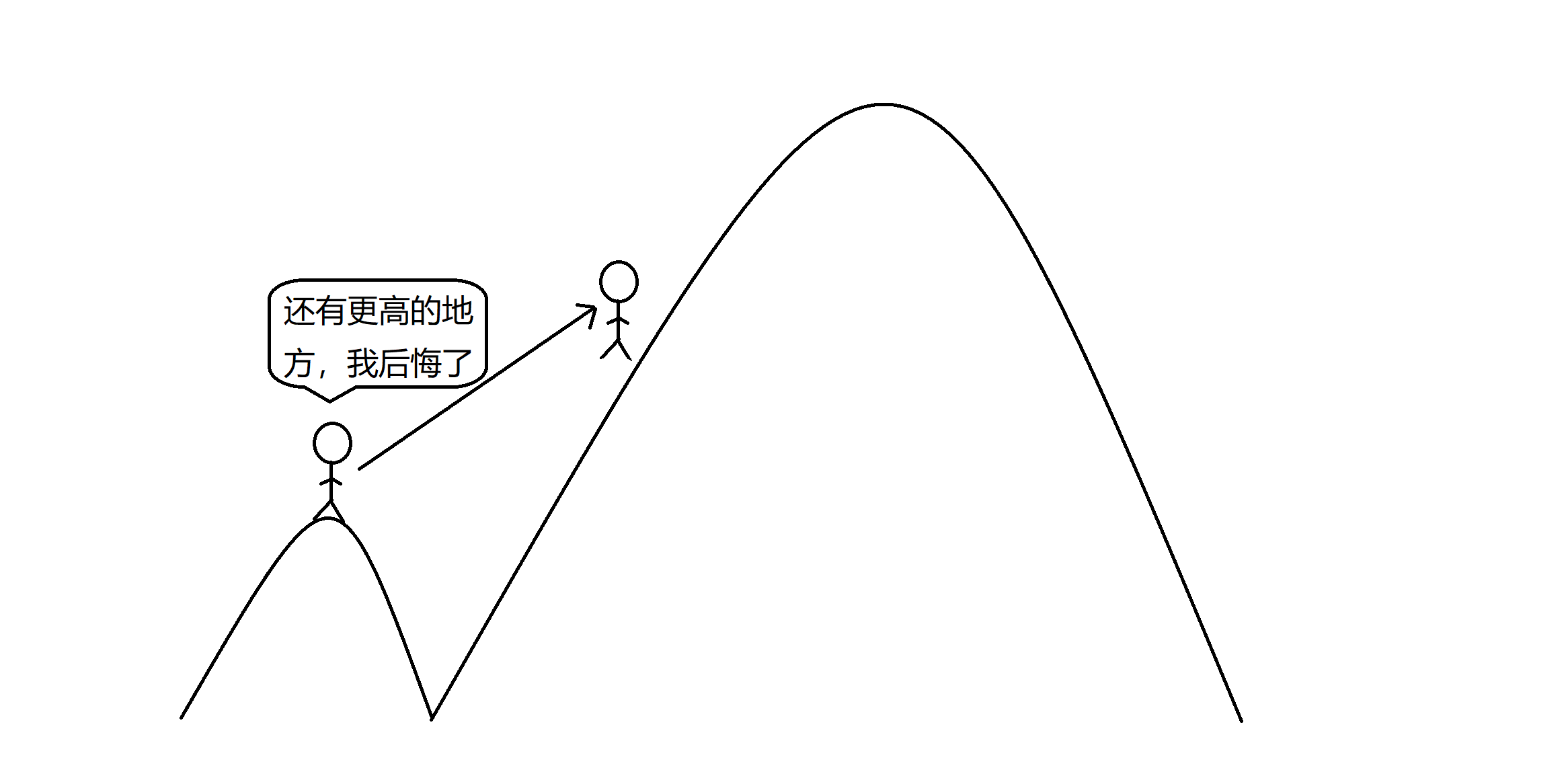
但是反悔贪心允许我们在发现现在不是全局最优解的情况下回退一步或若干步采取另外的策略去取得全局最优解。就好像我们站在的一座山的山峰上，看到了还有比我们现在所在位置还高的山峰，那我们现在就肯定不是在最高的地方了，这时我们就反悔——也就是下山再爬上那座更高的山：

分为两种基本方法：反悔堆和反悔自动机.

• 反悔堆：

  通过堆（大根堆、小根堆）来维护当前贪心策略的最优解，若发现最优解不对，就退回上一步，更新最优解。

  由于堆的性质，使得堆的首数据一定是最优的，这就可以实现快速更新最优解。

• 反悔自动机：

  设计一种反悔策略，使得任意一种贪心策略都可以得到正解。

  基本的设计思路是：每次选择直观上最接近全局最优解的贪心策略，若发现最优解不对，就想办法自动支持反悔策略。（这就是自动机的意思）

  具体题目具体分析。一般需要反悔自动机的题都是通过差值巧妙达到反悔的目的。本质上还是跑正常贪心。

反悔堆

P2949 [USACO09OPEN] Work Scheduling G

有 $n$ 项工作，$i$ 项工作有一个截止时间 $D_i$ ，完成每项工作可以得到利润 $P_i$ ，求最大可以得到多少利润。

这个题暴力的贪心，显然是按照 $D_i$ 排序之后贪心地选每个工作，直到选取的工作量 $= D_i$。但是考虑这样显然会漏掉很多工作，或者说因为选取了前面的一些低价值工作而导致后面的工作没有办法选。

所以我们考虑反悔，如何反悔？我们用一个小根堆储存前面的合法工作 $i$，每次考虑若当前工作 $P_i > $ 堆顶的 $P$(记选择的为 $x$)，那么就把 $x$ 这个决策换成 $i$。

合法性：因为我们按照 $D_i$ 排序之后肯定有 $D_i \geq D_x$，所以把 $x$ 换成 $i$ 不会影响答案的合法性。

最优性：我们用 $i$ 这个局部最优不断去替换此前的局部最优 $x$，当所有替换完毕之后就得到了全局最优。

/*
Undo the destiny.
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define pll pair<ll,ll>
#define mp make_pair

const int N = 1e5 + 10;
struct node {
    ll ddl,val;
    friend bool operator < (const node &a,const node &b) {
        if (a.ddl == b.ddl) return a.val > b.val;
        else return a.ddl < b.ddl;
    }
}p[N];
priority_queue <ll,vector <ll>,greater<ll> > q;
int n;

void solve() {
    cin >> n;
    for (int i = 1;i <= n;++i) cin >> p[i].ddl >> p[i].val;
    sort(p + 1,p+1+n);
    for (int i = 1;i <= n;++i) {
        if (q.size() < p[i].ddl) {
            q.push(p[i].val);
        } else {
            if (p[i].val > q.top()) {
                q.pop();
                q.push(p[i].val);

            }
        }
    }
    ll ans = 0;
    while (!q.empty()) {
        ans += q.top();q.pop();
    }
    cout << ans;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int T = 1;//cin >> T;
    while (T--) solve();
    return 0;
}

CF2085D

刚刚发现了一家回转寿司自助餐厅。所谓 “回转寿司”，是指餐厅里有一条传送带，将一盘盘寿司送到顾客薮猫面前。

在这家餐厅里，每盘寿司都有 $k$ 个， 第 $i$ 盘，美味度为 $d_i$ 。薮猫将在这家餐厅用餐$n$ 分钟，在这 $n$ 分钟内，他必须吃完从传送带上取下的所有寿司。

未吃完寿司的计数器记为 $r$ 。最初为 $r=0$ 。在 $i$ ( $1\leq i\leq n$ )分钟内，只有 $i$ ( $i$ )盘寿司会送到薮猫面前，他可以做以下中的一个：

• 从腰带上取下 $i$ (美味度为 $d_i$ ) 的寿司， $r$ 将增加 $k$ ；
• 吃掉他之前从腰带上取下的一块未吃完的寿司， $r$ 将减少 $1$ 。请注意，只有在 $r>0$ 的情况下才能这样做；
• 或者什么都不做， $r$ 将保持不变。

请注意， $n$ 分钟后， $r$ 的值必须为 $0$ 。

薮想要最大化他所拿的所有盘子的美味总和。帮他找出答案！

就是这个 byd 题让我写这份的。

实际上发现这个题的模型和上一题本质一样，我们这里反着做，也就保证了可以替换的正确性。然后直接贪心即可。

没写出来这个掉分了哈哈

/*
Am I allowed to cry?
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define pll pair<ll,ll>
#define mp make_pair
#define int long long
const int N = 5e5 + 10;
int n,k,a[N];
void solve() {
    priority_queue <int,vector <int>,greater<int> > q;
    cin >> n >> k;
    for (int i = 1;i <= n;++i) cin >> a[i];
    int res = 0;
    for (int i = n;i >= 1;--i) {
        ++res;
        if (res > k) {
            res -= k+1;
            q.push(a[i]);
        } else {
            if (!q.empty()) {
                if (a[i] > q.top()) {
                    q.pop();q.push(a[i]);
                }
            }
        }
    }
    int ans = 0;
    while (!q.empty()) {
        ans += q.top();q.pop();
    }
    cout << ans << "\n";
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int T;cin >> T;
    while (T--) solve();
    return 0;
}

P4053 JSOI2007 建筑抢修

有 $n$ 个任务，并且每个任务都有两个属性——截止日期和完成耗时。在截止日期前完成任务就可以得到这个任务产生的价值。在同一时间我们只能去做一个任务。所有任务的价值都是一样的，问我们最后最多能完成多少个任务。

由于我们需要反悔操作，而反悔操作是建立我们能够反悔——不做之前决定做的任务而去做当今决定做的任务，所以首先我们肯定还是要按照截止日期从小到大进行排序。

在我们上面讲到的用时一定的模型中，我们用堆维护“性价比”最低的任务也就是我们价值最低的任务用于反悔操作。在这个问题中，我们同样用堆去维护“性价比”最低的任务。由于每个任务的价值是一定的，所以我们性价比最低的任务就是耗时最长的任务，如果我们不做耗时比较长的任务去做耗时比较短的任务，我们就能留下更多的时间给后面的任务，又由于每个任务的价值是一样的，所以这样做的正确性也是显然的。

所以具体来说我们就开一个大根堆维护已选任务的时间，堆顶就是耗时最长的任务。我们顺次考虑排序后的每个任务，当前决定要做的任务的总耗时加上现在这个任务的耗时小于等于现在这个任务的截止时间，那我们就直接做，把现在这个任务丢进堆里，总耗时加上现在这个任务的耗时就可以了。但如果当前决定要做的任务的总耗时加上现在这个任务的耗时大于现在这个任务的截止时间呢，我们就考虑是否进行反悔操作替换决定做的任务。我们看一看堆顶任务的耗时和现在这个任务的耗时，如果堆顶任务的小那就不替换；如果当前任务的耗时小，我们就用当前任务替换掉堆顶任务就好啦。

/*
Undo the destiny.
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define pll pair<ll,ll>
#define mp make_pair
const int N = 2e5 + 10;
struct node {
    ll tim,ddl;
    friend bool operator < (const node &a,const node &b) {
        return a.tim < b.tim;
    }
}a[N];
bool cmp(node a,node b) {
    return a.ddl < b.ddl;
}
int n;
priority_queue <node> q;
void solve() {
    cin >> n;
    for (int i = 1;i <= n;++i) cin >> a[i].tim >> a[i].ddl;
    sort(a+1,a+1+n,cmp);
    ll lst = 0;
    // cout << q.size() << "\n";
    for (int i = 1;i <= n;++i) {
        if (lst + a[i].tim <= a[i].ddl) {
            q.push(a[i]);
            lst += a[i].tim;
        } else {
            if (a[i].tim < q.top().tim) {
                lst -= q.top().tim;q.pop();
                q.push(a[i]);lst += a[i].tim;
            }
        }
    }
    cout << q.size();
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int T = 1;//cin >> T;
    while (T--) solve();
    return 0;
}

反悔自动机

基本的设计思路是：每次选择当前直观上最接近最优解的方案。然后想办法怎么支持自动反悔。也就是我们在贪心的过程中实际上就进行了反悔这个操作。

Problem - D - Codeforces

已知接下来 $n$ 天的股票价格，每天可以买入当天的股票，卖出已有的股票，或者什么都不做，求 $n$ 天之后最大的利润。

我们尝试去考虑设计一种反悔策略，使所有的贪心情况都可以得到全局最优解。（即设计反悔自动机的反悔策略）

定义 $C_{buy}$ 为全局最优解中买入当天的价格，$C_{sell}$ 为全局最优解中卖出当天的价格，则：
$$
C_{sell}−C_{buy}=(C_{sell}−C_i)+(C_i−C_{buy})
$$
$C_i$ 为任意一天的股票价格

即我们买价格最小的股票去卖价格最大的股票，以期得到最大的利润。我们先把当前的价格放入小根堆一次（这次是以上文的贪心策略贪心），判断当前的价格是否比堆顶大，若是比其大，我们就将差值计入全局最优解，再将当前的价格放入小根堆（这次是反悔操作）。相当于我们把当前的股票价格若不是最优解，就没有用，最后可以得到全局最优解。

上面的等式即被称为反悔自动机的反悔策略，因为我们并没有反复更新全局最优解，而是通过差值消去中间项的方法快速得到的全局最优解。

/*
Undo the destiny.
*/
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}
#define pii pair<int,int>
#define pll pair<ll,ll>
#define mp make_pair
const int N = 3e5 + 10;
int n,a[N];
void solve() {
    priority_queue <ll,vector <ll>,greater<ll> > q;
    cin >> n;
    for (int i = 1;i <= n;++i) cin >> a[i];
    ll ans = 0;
    for (int i = 1;i <= n;++i) {
        q.push(a[i]);
        if (!q.empty() && q.top() < a[i]) {
            ans += a[i] - q.top();q.pop();
            q.push(a[i]);
        }
    }
    cout << ans;
}

signed main() {
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    int T = 1;//cin >> T;
    while (T--) solve();
    return 0;
}