线段树分块 Pro Max

关注嘉然喵，关注嘉然谢谢喵。

线段树基础

CF671E

知识点：楼房重建类线段树

我们首先考虑转化一下，这个问题就是 $n$ 点 $n-1$ 边，边负权点正权。先考虑原始问题，如何判断一个 $[l,r]$ 是符合条件的？

可以写出这个区间的贡献：$g_l - w_l +g_{l+1}\dots +g_r$ 也就是所有前缀和后缀和 $\geq 0$。

接着考虑加 $k$ 的想法，我们能让一个不合法区间变成合法的，首先可以用折线图表示：

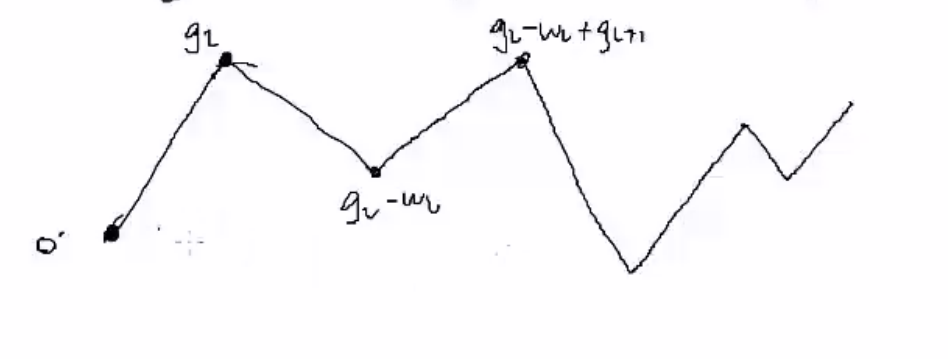
想让前缀和 $\geq 0$ 那么就是所有点都在 0 这条横线的上方。后缀和也就是翻转过来同样考虑。这样我们就刻画出来了两条横线，所有点都需要在两条线之间。

我们考虑贪心，扫到第一个前缀和小于 0 的位置，对其 +1，含义就是把后面所有点都抬高。但是我们不能放太前面，我们只对于某个 $\leq 0$ 的位置前面的一个 $g$ 进行加直到下一个位置变成 $0$。这样我们就能满足前缀条件。对于后缀条件，我们考虑把 $g_r$ 的位置变成最高的位置减去它的位置，合法性就是这两部分的和 $\leq k$.

接下来我们就考虑从小到大扫描线，我们枚举一个 $l$ ，然后求 $r$ 的最大值。

• 对于前缀来说：我们用一个 $b$ 记录最大值，我们影响的是后缀代价，也就是 $r$ 在这个位置及以后的 $a_i$ 需要加上 $c$。后缀 $b_i$ 的值加上 $c$。
• 对于后缀来说：代价为 $\max\limits_{l \leq r} (b_l) - b_r$

所以我们可以上线段树！对于第一步我们直接维护，第二步我们不直接维护，设第一个的后缀代价为 $a$，那么就是要求
$$
a_r +\max\limits_{l \leq r} (b_l) - b_r \leq k
$$
里面 $r$ 的最大值。

我们发现 $a,b$ 是同时加的，所以我们对于上面那个式子实际上是不用管的，所以我们只需要做两个事情。

1. 对于 $b$ 区间加
2. 查询 $\max\limits_{r \geq l}(b_l) - premax_r \leq k$ 中 $r$ 最大值

下面这个问题就是楼房重建类线段树了。

具体来说，我们考虑一个线段树，对于一个区间节点是 $[l,r,t]$ ，其中 $t$ 表示前缀最大值。那么我们对于上面的东西我们需要考虑快速查询 $premax_r$，如果 $\max(t,b_l,\dots,b_{mid}) \leq k$ 我们就直接找一个右子树就行。

那么还有一种情况是大于，那么就不可以预处理了，但是发现左子树里这个前缀和肯定都 $=t$ ，所以我们只要查询一个左子树的 $\max$，所以可以证明每种情况都只会去一个子树。整个过程是一个线段树二分的过程。

对于修改操作，我们的时间复杂度是 $\mathcal O (\log^2 n)$ 的。

「JOISC 2019 Day3」穿越时空 Bitaro

考虑怎么用线段树来维护这个信息，我们可以把所有的开放区间全部减去 $i$，就直接把时间轴这一维给抹掉了。

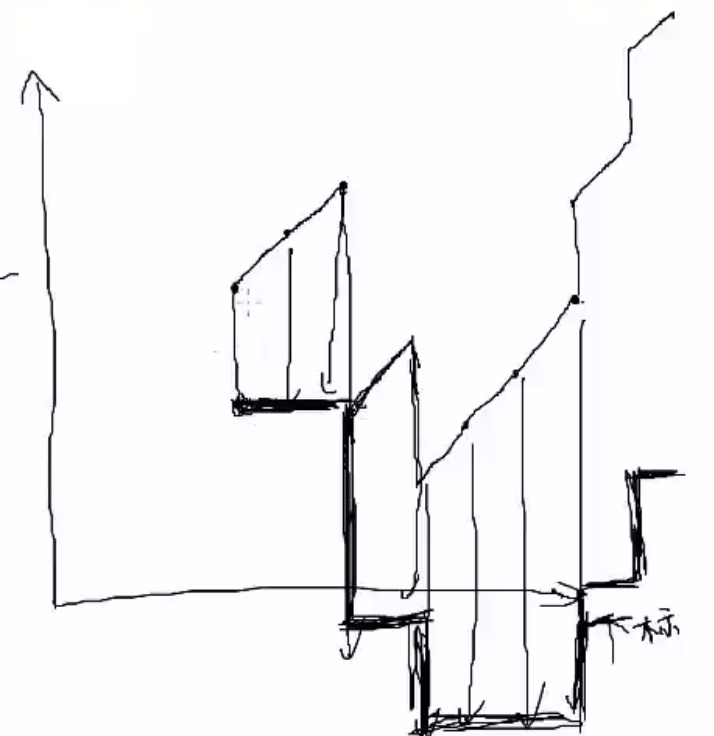
如果要经过边 $i$，我们就需要出发时间在 $[l_i,r_i]$ 里。只考虑从左往右走，现在这个问题就是我们可以往右走往下走，让往下走的总距离和最小。

我我们注意到，在一个位置多等一会显然不如少等一会，感性理解就是现在回溯不如以后回溯。

现在就有一个 $qn$ 的做法，我们每次贪心维护一串。维护两个函数，分别对应进入时间和出去时间以及代价，考虑几种情况。

1. 所有区间的交非空，设交为 $[l,r]$ ，我们就直接暴力让当前时间满足条件就行。

2. 所有区间的交为空，发现我们出去的时候位置是基本固定的，那么我们总可以认为穿过这段区间的效果是：初始时刻 $a$ ，到达时刻 $b$ ，必须使用 $k$ 次技能。

   这是因为我们可以在过区间的时候，将穿过后的一些技能平移到穿过前，这样我们的初始时刻就是相同的；同样也可以将穿过前的平移到穿过后，这样到达时刻就是相同的。

我们把第一类记为 A 点，第二类记为 B 点。B 点我们维护一个三元组 $(a,b,k)$ 含义同上，然后我们就维护一下 A 点 B 点合并就行。

CF1693E

/shui

我们从大往小考虑，对于一个 $i$ 考虑有多少书一次操作后变成 $i$，答案就是 $\sum a_i$。这个的意思是如果一个数 $\geq i$ 那么一定会变成 $i$ 的。我们前后缀考虑，如果把 $j$ 取前缀，我们会变成 $k$，否则取后缀会变成 $i$.

segbeats

介绍

Segment Tree Beats 学习笔记 - Neal_lee - 博客园 (cnblogs.com)

支持两种操作：

1. 区间 check min
2. 区间加

我们考虑记录区间中最大值，严格次大值，最大值个数，和。

考虑check min的 $c$：

1. $c \geq max$ 无事发生。
2. $secmax\leq c \leq max$ 所有 max 变成 c，sum += (c - mx) * num
3. $c \leq secmax$ 递归两子树，pushup

考虑对复杂度进行势能分析！带区间修改是 $log^2$ ，不带是 $\log$ 的

void update(int x, int l, int r, int L, int R, int val){
    if(t[x].mx <= val) return;
    if(l >= L && r <= R && t[x].smx < val){ addtag(x, val); return; }
    int mid = (l+r)>>1;
    pushdown(x);
    if(mid >= L) update(x*2, l, mid, L, R, val);
    if(mid < R) update(x*2+1, mid+1, r, L, R, val);
    pushup(x);
}

例题 CF1290E

对于每个子树的大小，我们考虑为 i 左侧第一个大于 ai 的位置 - i 左侧第一个大于 ai 的位置 - 1

那么分开来算，我们以第一个为例，第二个是对称的。

从 1-i 来算

线段树分裂

支持三种操作：

1. 区间正序排列
2. 区间倒序排列
3. 区间和

用 treap 维护所有连续段，再用权值线段树维护所有连续段的值

我们每次做区间修改的时候，每次用线段树分裂把当前块分成小块，对于大部块merge。

莫队

“大家都会！”

扫描线

B 维正交范围

在一个 B 维直角坐标系下，第 $i$ 维坐标在一个整数范围 $[l_i,r_i]$ 范围内。

A-side

理解为前缀。

一维扫描线

用扫描线扫一维，用 DS 维护另一维。

扫过去的过程中会 DS 维护的那一维上产生一些修改和查询。

查询信息可以差分就直接差分（二维数点），否则就需要分治了。

另一个角度就是序列角度，一维扫过去枚举右端点，DS 维护的是左端点答案。个人比较喜欢下面这种表达。

一般来说，能差分的题就尽量差分，问题第一维实际上是降低了自由度，让问题简单了很多!典型的差分方法：

• $[l,r]$ 差分为 $[1,r] - [1,l-1]$，两个前缀和
• 树上差分
• 二维前缀和差分

BZOJ3489

这个是一类问题的反演，反演的问题类型：

1. 平面上 $n$ 个点，$m$ 次询问矩形内有多少点。
2. 平面上 $n$ 个矩形，$m$ 次询问每个点上有多少矩形。

对于这个题就是考虑每个点对哪些区间有贡献，那么就是算每个值对每个区间的贡献。我们称本题询问的这种值称为色数。

我们要维护的实际上是一个 4-side 的矩形。

TEST_73

考虑点连通块就是 点 - 边 的个数。我们考虑边数，边数需要满足三个条件：两个端点，边的编号都在 $[l,r]$ 之间。

我们反演一下问题，计算每条边对答案的贡献，得到一个三维问题。发现我们只需要 $\min{a,b,c},\max{a,b,c}$ 这样就只需要做二维数点了！

这题启发是要好好研究问题，否则会造成问题的升维。

BZOJ4212

考虑建 trie，前缀就是 trie 上对应的子树，后缀就是反着建同理。

这个同时的约束，我们把问题拓展到二维，实际上就是查询有多少 $x$ 满足在第一个子树里，又在第二个子树里。

子树问题我们可以直接上 DFS 序，就变成一个二维数点了。

UOJ637

这类关于颜色数的问题，我们都考虑利用不同值对答案贡献独立的性质。

对每个元素，我们计算一下它对哪些询问有贡献，然后用DS维护。

我们考虑这个询问被哪些元素不包含。

CometOJ contest14D

还是构造二维平面，一维是操作位置，一维是原来序列的位置。

假设区间对 $[l,r]$ 进行染色，那么贡献是 3-side 的。

区间子区间问题

待补

CF526F

转化后题意：给排列，求有多少区间满足 $\max\limits_{l\leq i\leq r}{a_i} - \min\limits_{l\leq i\leq r}{a_i} = r - l$

还是想能不能转化成矩形，

掉线了，学弟说可以析合树！

CF997E

我们把 $l,r$ 分别当成 $x,y$ 轴，那么子区间就是转换为查询一个矩形内有多少点满足某条件，是一个三角部分。

可以看作是一个2-side矩形。