计算几何笔记

二维基础

点

可以用 int 解决的尽量用 int 解决。

如果用处不多的时候可以用 pair<double,double>，但是更多时候还是：

struct Point {double x,y;};

向量

点积：$\vec{a} · \vec{b} = a_xb_x+a_yb_y$ 几何意义：$\vec{a}·\vec{b} = |\vec{a}||\vec{b}|\cos \theta $

求长度：$|\vec{a}| = \sqrt{\vec{a}·\vec{a}}$ 投影：$|\vec{a}| \cos\theta= \frac{\vec{a}·\vec{b}}{|\vec{b}|}$

叉积：$\vec{a}\times \vec{b} = (a_xb_y-a_yb_x)$ 几何意义：$\vec{a}\times \vec{b} = |\vec{a}| |\vec{b}| \sin\theta$

求平行四边形面积：直接 $| \vec{a}\times \vec{b} | = | |\vec{a}| |\vec{b}| \sin\theta | $ 三角形的面积记得带上 $\frac{1}{2}$

判断向量平行：$\vec{a}\times\vec{b} = \vec{0}$

to-left 测试：判断点和直线的位置关系

• $\vec{AB}\times \vec{AP} > 0$，$P$ 在有向直线 $AB$ 左侧。
• $\vec{AB}\times \vec{AP} < 0$，$P$ 在有向直线 $AB$ 右侧。
• $\vec{AB}\times \vec{AP} = 0$，$P$ 在有向直线 $AB$ 上。

本质：右手法则

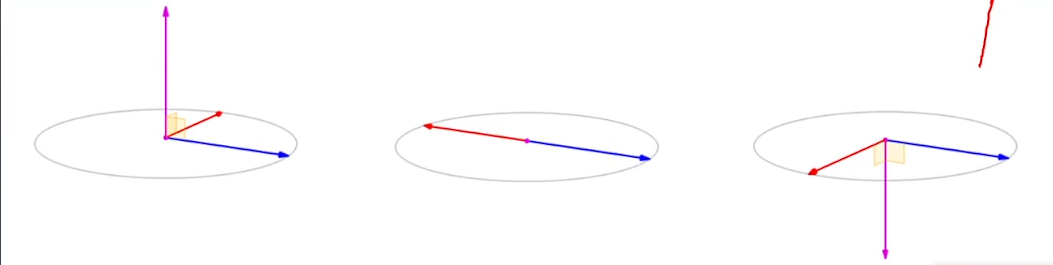
向量旋转：把向量 $\vec{a}$ 逆时针旋转 $\theta$ 是什么？

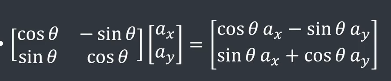
$a_x = \cos\theta a_x-\sin{\theta}a_y,a_y = \sin\theta a_x+\cos{\theta}a_y$’’

点和线段的关系：考虑 $P$ 与线段 $AB$ 的关系

$P$ 在 $AB$ 所在直线上：$\vec{PA}\times\vec{PB} = \vec{0}$

$P$ 在 $AB$ 之间：$\vec{PA}\times\vec{PB} \leq \vec{0}$

线段与线段的关系：考虑线段 $AB$ 与线段 $CD$ 的关系，判断二者是否相交

考虑跨立实验，判断 $A,B$ 是否在 $CD$ 的不同侧， $C,D$ 是否在 $AB$ 的不同侧

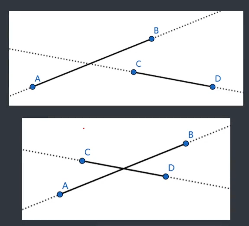
但是关键在于，可能存在 $AB,CD$ 共线的情况。记得判断点是否在线段上，以及区间是否相交。

直线

点向式：记直线上一点 $P$，方向向量 $\vec{v}$，$(x,y) = \vec{OP} + \lambda \vec{v}$

struct Line {Point p,v;};

点到直线的距离：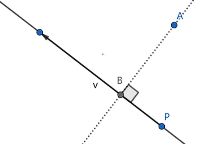

利用一下简单的高中数学：$|\vec{AB}| = |\vec{PA}| |\sin\theta| = \frac{|\vec{v}\times\vec{PA}|}{|\vec{v}|}$

点在直线上的投影点：

如何避免开方？

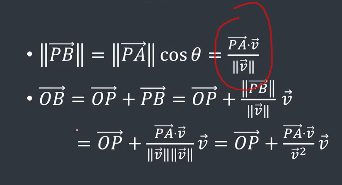
多边形

struct Polygon {vector <Point> p;};

注意首尾两个点。

面积：分解成若干三角形的面积

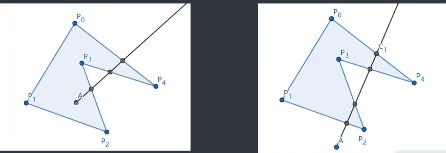
$S = \frac{1}{2}|\sum\limits_{i=0}^{n-1} \vec{OP_i}\times \vec{OP_{i+1 \bmod n}}|$ 注意到即使 $O$ 在多边形外，实际上也依然成立：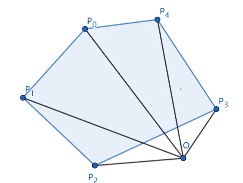

图中 $O$ 与 $P_1,P_0,P_4$ 的叉积是正的， 然后注意到 $OP_2,OP_3$ 的叉积是负的，利用割补法面积仍然成立。

判断点是否在多边形内：光线投射算法

从点引出一条射线，如果射线与多边形有奇数个交点，那么该点在多边形内部，否则该点在多边形外部。