CF1039D You Are Given a Tree 解题报告

CF1039D You Are Given a Tree

有一棵 $n$ 个节点的树。

其中一个简单路径的集合被称为 $k$ 合法当且仅当：

树的每个节点至多属于其中一条路径，且每条路径恰好包含 $k$ 个点。

对于 $k\in [1,n]$，求出 $k$ 合法路径集合的最多路径数
即：设 $k$ 合法路径集合为 $S$，求最大的 $|S|$。

$n \leq 10^5$

解题思路：

分治（整体二分）。

首先可以观察一下这个问题的一些性质，很显然，我们考虑对于这个合法路径的答案取值其实最多只有 $\sqrt{n}$ 种并且具有单调性，这个的证明非常显然，类似数论分块的证明。

接下来想下暴力怎么做，我们对于单独的一个 $k$ 来考虑。首先，每个点最多只可能在一条链中，这给我们贪心提供了一个正确性的保证。对于一个点，如果当前点有一条拐弯的最长链长度大于等于 $k$ ，我们就贪心划分成一条答案所需要的链。

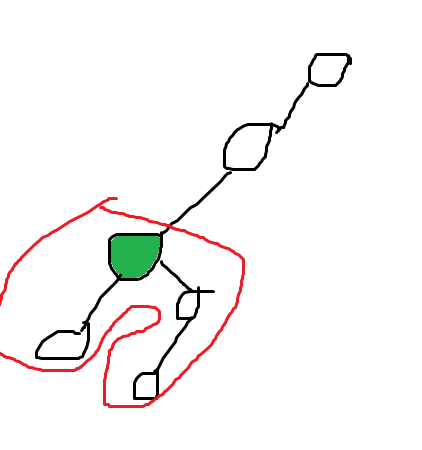
如图，红色圈起来的就是一条拐弯的最长链。

否则，我们这个节点保存一个不拐弯的最长链长度 $f_x$ 以供接下来使用。

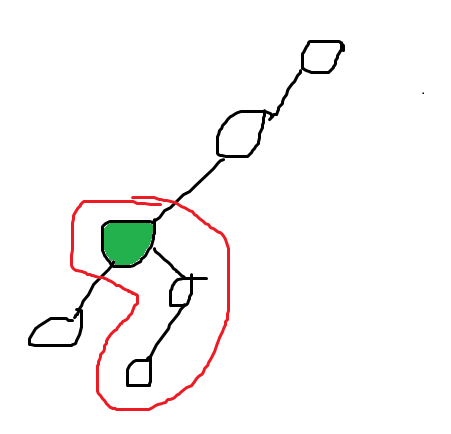
如图，红色圈起来的就是一条不拐弯的最长链。

接下来考虑分治，有点类似整体二分（其实我个人是按整体二分来理解的，但是被机房学长纠正说不是整体二分），在分治过程中，我们对于 $k \in [L,R]$ ，答案属于 $[l,r]$ 的询问进行分治。每次选取 $mid = \lfloor \frac{L+R}{2}\rfloor$ 进行 dfs，得出的答案记为 $tmp$，那么对于 $k \in [L,mid]$ 来说，答案属于 $[l,tmp]$，对于 $k \in [mid + 1,R]$ 来说，答案属于 $[tmp,r]$ ，当 $l = r$ 时，我们就将 $[L,R]$ 的答案全部赋为 $l$。

这样，我们的时间复杂度就做到了 $\mathcal{O}(n \sqrt{n} \log n)$，这个复杂度感性理解即可（因为我也不会证是机房学长告诉我的orz，如果有dalao会证也可以在评论区，目前的想法是分治树有 $\log n$ 层，答案有 $\sqrt{n}$ 个，分治的过程就是 $n \log n \times \sqrt{n}$ ）

注意这个东西常数非常大……你需要一些卡常技巧，这里提供一个亲测能过的。首先把原图存下来，然后 dfs 一遍，确定每个点的父子关系，然后只保存从父亲到儿子的边，能快一半以上，具体可以看代码。

代码：

const int N = 1e5 + 10;

int n,ans[N],f[N],cnt;
vector <int> G[N];
int hd[N],nxt[N<<1],to[N<<1],tot;

inline void addedge(int u,int v) {
	to[++tot] = v;nxt[tot] = hd[u];hd[u] = tot;
}

void dfs(int x,int fa,int k) {
    f[x] = 0;
    int maxx = 0,secmax = 0;
    for (int i = hd[x];i;i = nxt[i]) {
        int y= to[i];
        if (y != fa) {
            dfs(y,x,k);
            if (f[y] > maxx) {
                secmax = maxx;
                maxx = f[y];
            } else {
                secmax = max(secmax,f[y]);
            }
        }
    }
    if (maxx + secmax + 1 >= k) ++cnt,f[x] = 0;
    else f[x] = maxx + 1;
}

void solve(int l,int r,int L,int R) {
    if (l > r || L > R) return ;
    if (L == R) {
        for (int i = l;i <= r;++i) {
            ans[i] = L;
        }//sqrtn
        return ;
    }
    int mid = (l + r) >> 1;
    cnt = 0;
    dfs(1,0,mid);
    ans[mid] = cnt;
    solve(l,mid - 1,cnt,R);//越短越多.
    solve(mid + 1,r,L,cnt);
}

void prework(int x,int fa) {
    for (auto y : G[x]) {
        if (y != fa) {
            addedge(x,y);
            prework(y,x);
        }
    }
}

signed main() {
    read(n);
    for (int i = 1;i < n;++i) {
        int x,y;read(x);read(y);
        G[x].push_back(y);
        G[y].push_back(x);
    }
    prework(1,0);
    solve(1,n,0,n);
    for (int i = 1;i <= n;++i) writeln(ans[i]);
}