Luogu P2458 [SDOI2006]保安站岗 解题报告

P2458 [SDOI2006]保安站岗

有一棵无根树有 $n$ 个点，每个点都可以被其相邻的点望到。

每个点带有一个权值，求保证所有点都可以被望到的情况下花费总代价最少。

解题思路：

树形 DP。

最开始我的想法和树上最小点覆盖的想法一样，每个点有选与不选两种状态，暴力转移。

成功拿到 10 分。

回到正题，这题和树上最小点覆盖的本质区别在于：

• 树上最小点覆盖每个点只能被父亲看见
• 本题中的每个点可以被父亲或者儿子看见

所以直接导致我们的状态不再适用。

那么怎么办呢？可以暴力直接把这种情况加进去！

同样，我们设 $f_{i,0/1/2}$ 表示第 $i$ 个点的情况：

• 如果是 0 ，表示当前点被选中
• 如果是 1 ，表示当前点是被父亲看到的，且当前点未被选中
• 如果是 2 ，表示当前点是被儿子看到的，且当前点未被选中

前两种情况的转移方程很好写，考虑可行性即可。

$$f_{x,0} = \min_{y \in son(x)}(f_{y,0,}f_{y,1},f_{y,2})$$

因为该点被选中，所以子节点怎么转移都行

$$f_{x,1} = \min_{y \in son(x)}(f_{y,0},f_{y,2})$$

因为该点没被选中，所以子节点中 $f_{y,1}$ 就不能被转移。

最后一种情况似乎大同小异：

$$f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2})$$

但是，让我们考虑这样的一种情况：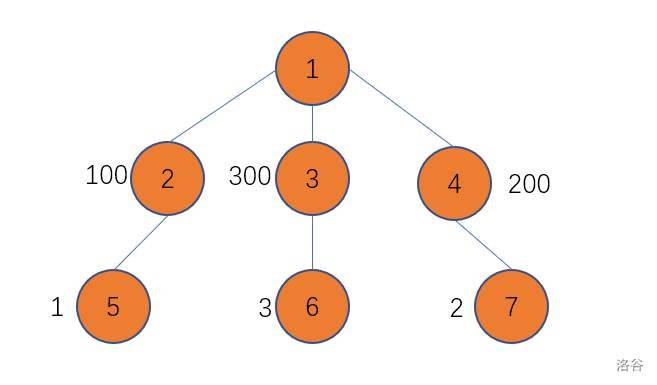

在这张图中，$f_{1,2} = f_{2,2}+f_{3,2}+f_{4,2}$ ，显然不符合状态的定义， $1$ 并没有被观察到，所以我们还要暴力选择一个$f_{y,0}-f_{y,2}$差值最小的点（上图中为 $2$）才能保证正确性。

所以我们就可以写出最后一种情况的方程了：

如果有选择 $f_{y,0}$，则

$$f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2})$$

如果没有，则

$$f_{x,2} = \min_{y \in son(x)}(f_{y,0},f_{y,2}) + \min_{y \in son(x)}(f_{y,0} - f_{y,2}))$$

这两个只要在代码实现时候记录下即可。

初值：$f_{x,0} = a_x,f_{x,1} = f_{x,2} = 0$

目标：$\min(f_{root,0},f_{root,2})$（根节点没有父亲，所以没有 $f_{root,1}$ 的情况）

最后，由于并没有指定根，所以读入时还要记一下入度为 0 的点当作根开始 DP。

代码：

省略头文件

int n,a[N],f[N][3],deg[N];
//f_{i,0} 表示当前点放一个 f_{i,1}表示父亲放 f_{i,2} 表示儿子放
//当前点放的话随便转移
//父亲点放的话可以转移到f_{y,0}或f_{y,2}
//儿子放的话要找到一个最小儿子 让放置儿子代价最小

void dfs(int x,int fa) {
	f[x][0] = 1;	
	int del = INF;//记录f_{y,0} - f_{y,2}的最小值
	bool flag = false;//记录是否选择全部不选
	for (int i = hd[x];i;i = nxt[i]) {
		int y = to[i];
		if (y == fa) continue;
		dfs(y,x);
		f[x][0] += std::min(f[y][0],std::min(f[y][1],f[y][2]));//第一种情况更新
		f[x][1] += std::min(f[y][0],f[y][2]);//第二种情况更新
		if (f[y][0] < f[y][2]) {
			f[x][2] += f[y][0];
			flag = true;//选择了f_{y,0}
		}
		else {
			del = std::min(del,f[y][0] - f[y][2]);//计算f_{y,0} - f_{y,2}的最小值
			f[x][2] += f[y][2];
		}
	}	
	if (!flag) {
		f[x][2] += del;//如果没有选择则暴力加上
	}
}



signed main() {
	read(n);
	for (int i = 1;i < n;++i) {
		int x;read(x);int y;read(y);
		addedge(x,y);
		deg[y]++;//记录每个点入度
	}
	int root = 0;
	for (int i = 1;i <= n;++i) if (!deg[i]) root = i;//记录根节点
	dfs(root,0);
	printf("%d\n", std::min(f[root][0],f[root][2]));
    //根节点没有父亲，所以不用转移f_{root,1}
	return 0;
}