Luogu P6397 [COI2008] GLASNICI 解题报告

P6397 [COI2008] GLASNICI

一条直线上有 $n$ 个信使，将他们按照从左至右的顺序以 $1$ 至 $n$ 编号。换句话说，设 $i$ 号信使的的坐标为 $d_i$，则对于 $1 \leq i \lt n$， $d_i \leq d_{i + 1}$。

信使传递一条消息的方法如下：

• 在任意时刻（不一定是整数时刻），任一信使（无论是否已知消息）都可以自由选择向左移动或者向右移动或者原地不动。其移动的速度为每秒 $1$ 单位长度。
• 当两个信使相距不超过一给定实数 $k$ 时，双方可以进行消息传递，也即如果两人中有一人已知该消息，则两人都知道了该消息。消息传递是瞬间发生的，不消耗时间。

现在 $1$ 号信使得到了一条消息，请求出最小的让所有信使都得到该消息的用时。

$1 \leq n \leq 10^5,0 \leq k \leq 10^6$

解题思路

很巧妙的思维题。

首先把问题转化一下,对于一个点 $x_i$,存在点能覆盖到 $x_i$ 的范围为 $[x_i-k,x_i+k]$。

可以画个图加以理解。

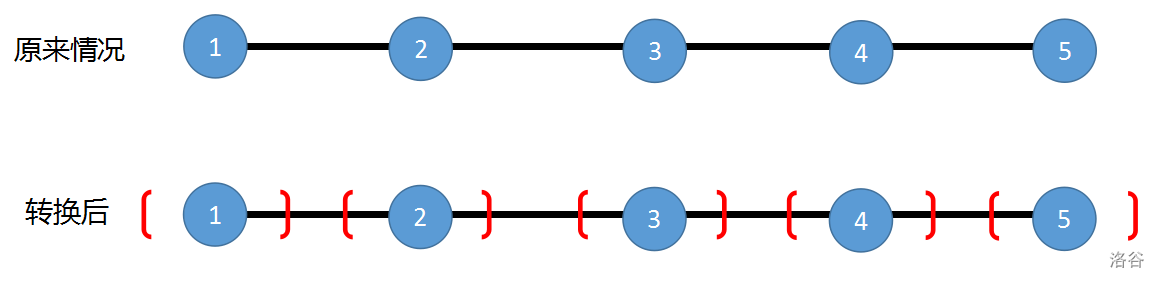
我们发现，这个用时肯定满足单调性，所以我们考虑二分。接着考虑边界，左边界肯定为 $0$，也就是所有点互相可以传信息的情况。右边界为 $x_n - x_1 - k$ 代表着 $x_1$ 要一直走到 $x_n-k$ 的位置。

关于实数域上的二分，我们可以这么写.

const double eps = 1e-6;//输出k位小数，eps最好设为10^(-k-2)
double l = 0.0,r = pos[n] - k - pos[1];
while (l + eps < r) {
    double mid = (l + r) / 2;
    if (check(mid)) r = mid;
    else l = mid;
}

接着考虑 check 怎么写。我们可以想一下两个点是如何相遇的：当前点 $i$ 往右走， 点 $i+1$ 往左走。注意到题目中是所有点都可以移动，所以为了保持相对位置不变，我们对于后面的点同时也要向左走。

结合图理解更佳。

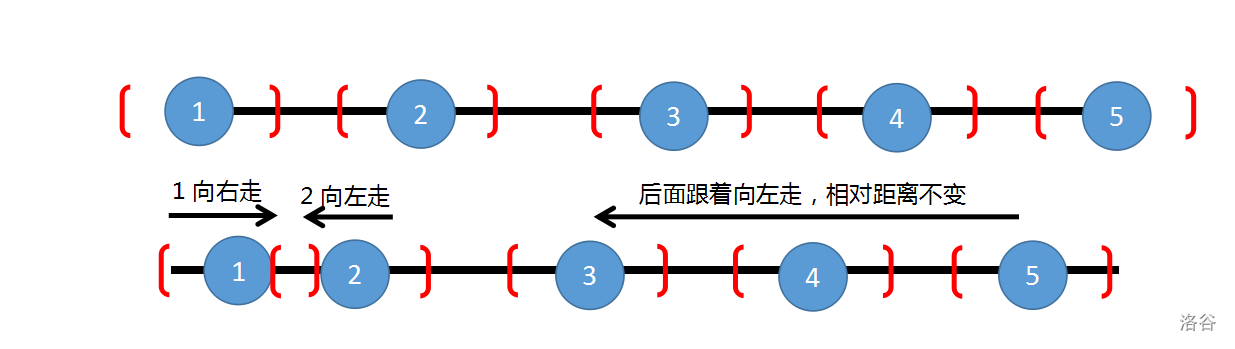
所以我们可以弄一个指针 $now$，表示当前能到达的最远地方。在最开始，我们贪心地让 $now = x_1 + k$，接下来有两种情况：

1. $now + k \geq x_{i+1}$ 这种情况就贪心的让 $now = now + k$
2. $now + k < x_{i+1}$ 这种情况我们没有办法，只能让 $now = x_i + k$
3. $now < x_i - k - mid$ 这样无论怎么都到达不了了， $mid$ 就肯定不能取到。

变成代码就是

bool check(double x) {
    double now = pos[1] + x;//初始化
    for (int i = 2;i <= n;++i) {
        if (pos[i] - k - now > x) return 0;//情况3
        now = min(now + k,pos[i] + x);//情况1和情况2
    }
    return 1;
}

所以我们就在 $O(n \log d)$ 的时间内解决了本题。

代码

#include <cstring>
#include <cstdio>
#include <cctype>
#include <cmath>
#include <algorithm>
using namespace std;
#define ll long long
#define ri register int

const int N = 100010;
const double eps = 1e-6;

double pos[N],k;

int n;

bool check(double x) {
    double now = pos[1] + x;
    for (int i = 2;i <= n;++i) {
        if (pos[i] - k - now > x) return 0;
        now = min(now + k,pos[i] + x);
    }
    return 1;
}

signed main() {
    scanf("%lf\n%d",&k,&n);
    for (int i = 1;i <= n;++i) scanf("%lf",&pos[i]);
    double l = 0.0,r = pos[n] - k - pos[1];
	while (l + eps < r) {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    printf("%.4f",l);
    return 0;
}