首先先研究一下 $a_i \not ={0}$ 的情况,我们先把操作记为 $(l_1,r_1),(l_2,r_2)$ 显然两个操作的代价分别是 $\frac{l_1 + r_1}{2},\frac{l_2 + r_2}{2}$
可以证明,如果 $(l_1,r_1),(l_2,r_2)$ 有交集,结果肯定不如选 $(\min(l_1,l_2),\max(r_1,r_2))$ 来的优。
简要证明一下:
第一种情况:$(l_2,r_2) \in (l_1,r_1)$ 如图:
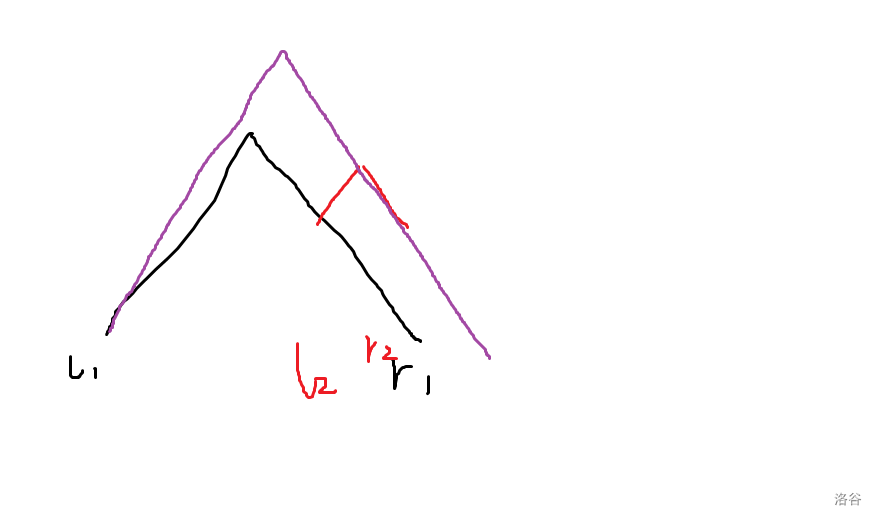
这里,选紫色的覆盖方式代价与 $(l_1,r_1),(l_2,r_2)$ 的代价相同,但是可以覆盖到更多的数。
第二种情况:$(l_2,r_2) \notin (l_1,r_1)$

同上。
所以我们不难写出 45 分代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| int las,nxt;++n;
for (int i = 1;i <= n;++i) {
if (a[i] && !a[i-1]) {
las = i;
continue;
}
if (!a[i]) {
if (!a[i-1]) continue;
nxt = i - 1;
ll tmp = 0x3f3f3f3f3f3f3f3f;
pre[las] = a[las] - las;suf[nxt] = a[nxt] + nxt;
for (int j = las + 1 ;j <= nxt;++j) pre[j] = max(pre[j-1],a[j] - j);
for (int j = nxt - 1 ;j >= las;--j) suf[j] = max(suf[j+1],a[j] + j);
for (int j = las ;j <= nxt;++j) tmp = min(tmp,max(pre[j] + j,suf[j] - j));
ans += tmp;
}
}
|
该算法的核心在于找出前缀最大后缀最大,然后选择这个位置。
那么存在 $0$ 的时候,显然整个东西会被分成若干个段,这些段之间选的点可能有交集,所以不能直接算。
但是交集启发我们可以通过判断区间交来合并,我们利用一个栈来完成这个工作,每做完一个非 $0$ 段之后就把区间与栈里的能合并的区间都合并到一起,代码很好写,时间复杂度 $O(n)$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| pii s[N];
int top,n,L,R;
ll ans;
signed main() {
read(n);
for (int i = 1;i <= n;++i) {
int x;read(x);
if (!x) continue;
int l = i - x,r = i + x;
if (l > R) {
s[++top] = make_pair(L,R);
L = l,R = r;
} else {
L = min(L,l),R = max(R,r);
while (L <= s[top].second && top) {
L = min(L,s[top--].first);
}
}
}
s[++top] = make_pair(L,R);
for (int i = 1;i <= top;++i) ans += (ll)(s[i].second - s[i].first + 1) / 2;
printf("%lld\n",ans);
return 0;
}
|
这种方法里使用的是不同的求非 $0$ 段方法,其实是等价的。

