2021.2.3 训练赛
A.Anniversary Cake
给你一个 $w\times h$ 的矩形,在矩形中有两个整点。请你找到一种方案将矩形划分成两个部分,每个部分中各有一个点。
$w,h \leq 10^9$
相对简单的构造题,大概在Div2A难度,考场上考虑比较simple所以挂了两发。
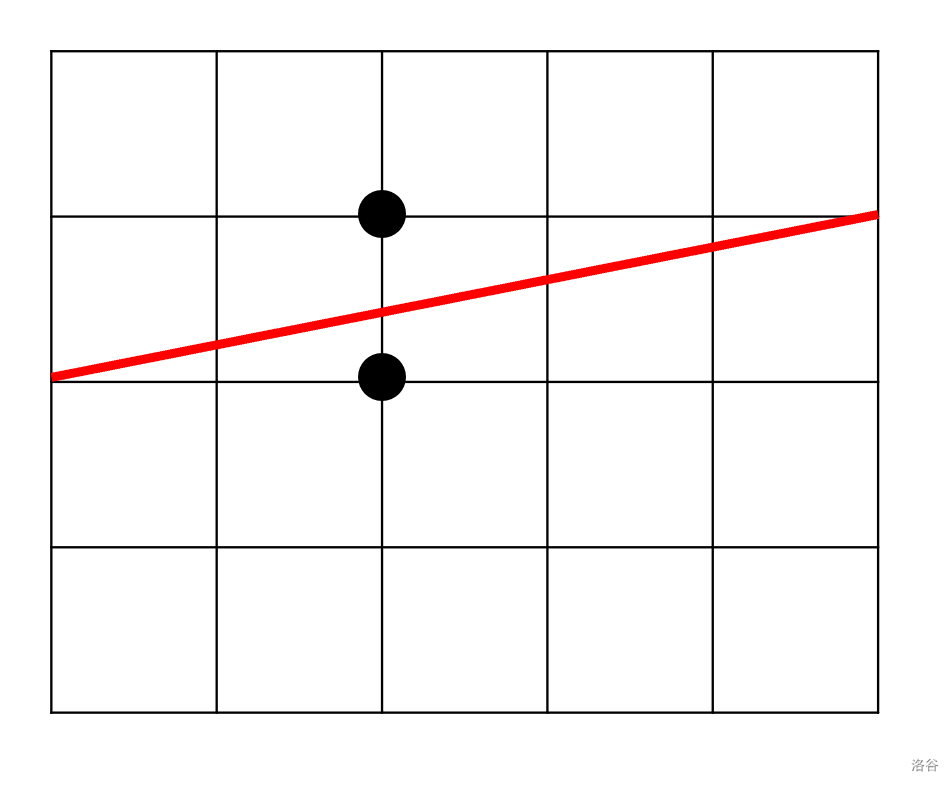
我们设两个点坐标为 $(x_1,y_1),(x_2,y_2)$ 一共有两种情况需要我们讨论,一种情况是横坐标相同,如图:
这种情况下,我们可以直接构造到两个点的最左和最右端,即 $(0,y_1),(w,y_2)$
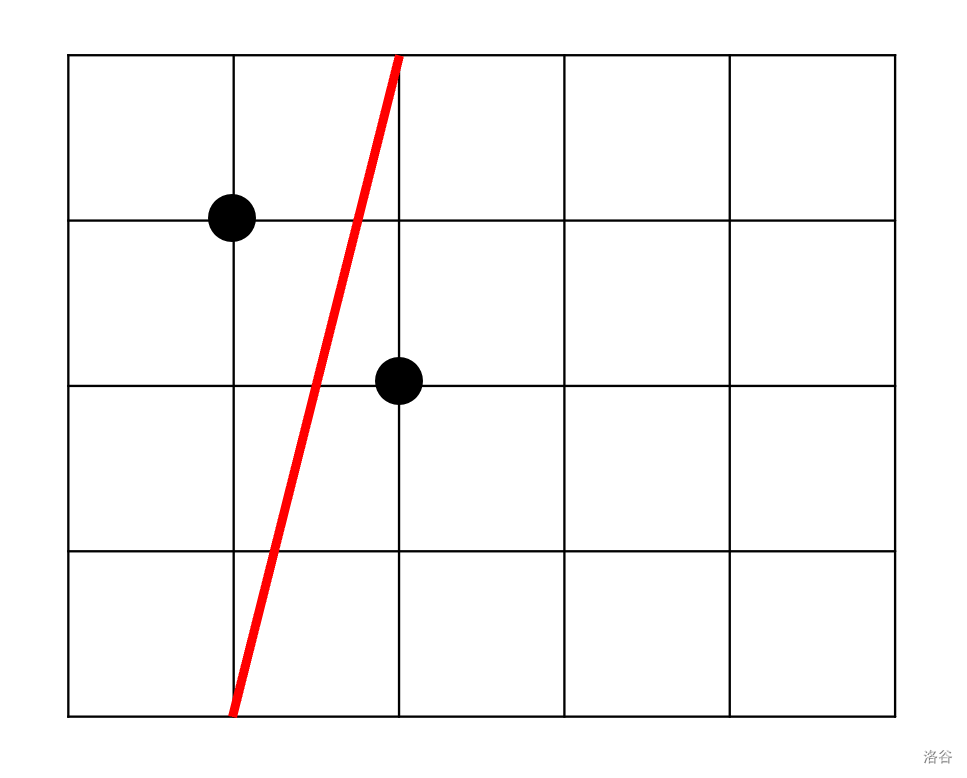
第二种情况就是横坐标不同,如图:
这种情况下,我们可以直接构造到两个点的最下和最上方,即 $(x_1,0),(x_2,h)$
想出方案后代码就很好写了。
Code:
1 2 3 4 5 6 7 signed main () read (w,h,x1,y1,x2,y2); if (x1 == x2) cout << 0 << " " << y1 << " " << w << " " << y2; else cout << x1 << " " << 0 << " " << x2 << " " << h; return 0 ; }
C.CodeCoder vs TopForces
有 $n$ 个人,每个人有两个能力值 $a_i$ 和 $b_i$。一个人能打败另一个人当且仅当这个人有一项或两项能力值都大于另一个人。也就是说当 A 比 B 强时可能有 B 比 A 强。
强的关系具有传递性,也就是说 A 比 B 强, B 比 C 强,那么 A 比 C 强。
$n \leq 10^5,a_i,b_i \leq 10^6$
这个题很有意思,初看你可能感觉这个是个排序题,后面挂了一发才发现这个题没有那么简单。
对于这种关系可传递的题,我们有一个比较直接的想法是可以将其建成一张有向图。比如我们把样例建图完就是下面的样子:
那么对于一个点 $i$,可以击败的人数就是 $i$ 的可达点数。
$O(n^2)$ 做法,对于每个点 dfs 一遍,得出每个点的可达点数量。
但是这样显然是过不去的,我们再从题目中观察条件。发现点 $i$ 可达点 $j$ 的要求是 $a_i > a_j$ 或 $b_i > b_j$。
我们就考虑能不能通过某些处理方法先优化掉一个条件。考虑如下的贪心策略:我们对于每个点按照 $a$ 或者 $b$ 排序(两个条件是等价的),然后对于每个 $b_i$ 较大的点,它前面的那些点是显然可达的。所以我们排序后依次 dfs,对于每个访问到的点打一个标记(后面的点肯定可以访问到),每次 dfs 都直接往答案中累加就行了。
Code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 struct node { int val,pos; }a[N],b[N]; int n;bool cmp (node p,node q) return p.val < q.val; } vector <int > G[N]; int vis[N],ans,orz[N];void dfs (int x) if (!vis[x]) ++ans; vis[x] = 1 ; for (int i = 0 ;i < G[x].size ();++i) { int y = G[x][i]; if (!vis[y]) dfs (y); } } signed main () read (n); for (int i = 1 ;i <= n;++i) { read (a[i].val,b[i].val); a[i].pos = i,b[i].pos = i; } sort (a+1 ,a+1 +n,cmp),sort (b+1 ,b+1 +n,cmp); for (int i = 2 ;i <= n;++i) { G[a[i].pos].push_back (a[i-1 ].pos),G[b[i].pos].push_back (b[i-1 ].pos); } for (int i = 1 ;i <= n;++i) { if (!vis[a[i].pos]) dfs (a[i].pos); orz[a[i].pos] = ans - 1 ; } for (int i = 1 ;i <= n;++i) { printf ("%d\n" ,orz[i]); } return 0 ; }
F.Folding
求一个 $W \times H$ 的矩形通过折叠变为一个 $w\times h$ 的矩形的最少折叠次数,其中每次折叠的折痕必须平行于矩形的一边。
$1\le W,H,w,h\le10^9$
场上队友写挂好几发被我撵下来了
首先这个题比较不喜欢的是它并没有保证长边和短边(队友就是在这里挂了好多发)所以先把短边和长边算出来,后文中提到的 $W,H,w,h$ 均保证 $W\leq H,w \leq h$,然后来讨论情况。
首先讨论无解的情况:显然,如果我们的最短边比目标最短边短,或者最长边比目标最长边短就无解了。你折纸总不可能越折越长对吧。
接着考虑有两种折叠情况:将 $W$ 变成 $w$,$H$ 变成 $h$。或者将 $W$ 变成 $h$,$H$ 变成 $w$.
所以代码就很好写了,我们不断用短边乘二靠近长边,统计次数即可。
Code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 int solve (int y,int x) if (x == y) return 0 ; int cnt = 0 ; while (1 ) { x *= 2 ;++cnt; if (x >= y) return cnt; } } signed main () int ans = 0 ; read (a,b,c,d); l1 = min (a,b),h1 = max (a,b),l2 = min (c,d),h2 = max (c,d); if (l2 > l1 || h2 > h1) { printf ("-1" );return 0 ; } ans = min (solve (l1,l2) + solve (h1,h2),solve (l1,h2) + solve (h1,l2)); printf ("%d" ,ans); return 0 ; }
G.Gangsters in Central City
每一次添加和移除后,你将要回答下面两个问题:
最少需要砍多少条边,才能使已选房屋都不能从根节点到达。
在第 $1$ 问的条件下,如何砍边使从根节点点开始走不能到达的非已选房屋数目最小,输出最小值。
$n \leq 10^5$
来补一个另外一个题解中说的神乎其神的 set 做法。
对于第一问,我们有个很简单的思考:我们显然只需要砍掉和根节点直接相关联的边即可满足最小。这个的证明十分显然,因为砍掉这些边显然能影响到的点是最多的。
然后我们来考虑第二问,一个最直接的想法:我们需要求出集合中靠的比较近的点的 LCA ,然后砍断这些 LCA 和父亲的连边。接下来就是两个问题:
哪些点算是集合中靠的比较近的点?
怎么找到多个点的 LCA?
第一个问题我们需要结合第一问来思考,第一问中,我们砍掉的都是直接和根节点关联的边,所以我们把集合中的点按照所属直接关联根节点的子树 来分类。可能有些抽象,结合代码来理解。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 void dfs2 (int x,int anc) bel[x] = anc; for (int i = 0 ;i < G[x].size ();++i) { int y = G[x][i]; dfs2 (y,anc); } } for (int i = 1 ;i < n;++i) { int x;cin >> x;G[x].push_back (i+1 ); deg[x]++; if (x == 1 ) lis.push_back (i+1 ); } for (int i = 0 ;i < lis.size ();++i) { dfs2 (lis[i],lis[i]); }
这样我们就把点按照从属的子树分成了几类。
第二个问题其实是之前刷知乎找到的,这里(如何在 DAG 中找多个点的 LCA ? - 阮行止的回答 - 知乎 )有非常详细的证明,不再赘述。这里直接丢结论:树上多个点的LCA,就是DFS序最小的和DFS序最大的这两个点的LCA。
所以我们对于每个子树内的点维护一个 set,每次取出 dfs 序最大点和 dfs 序最小点求出这些点的 LCA。我们可以算出砍掉一条边的代价为 这个点覆盖的叶子数 - 这棵子树里的被封锁节点数。
对于增加操作,我们先对于原来的 LCA 求出这个 LCA 控制的叶子节点数,再对插入点后的 LCA 求出这个 LCA 控制的叶子节点数,两者相减再扣去当前集合内的点数就是答案。
具体请看代码实现。
Code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 int bel[N];int rul[N],dfn[N],cnt,deg[N],vis[N],rk[N];int n,q;bool leaf[N];vector <int > G[N],lis; set <int > s[N]; void dfs1 (int x) dfn[x] = ++cnt;rk[cnt] = x; for (int i = 0 ;i < G[x].size ();++i) { int y = G[x][i]; dfs1 (y); } } int dfs2 (int x,int anc) bel[x] = anc; if (leaf[x]) { return rul[x] = 1 ; } for (int i = 0 ;i < G[x].size ();++i) { int y = G[x][i]; rul[x] += dfs2 (y,anc); } return rul[x]; } int dep[N],top[N],siz[N],fat[N],son[N],ans1,ans2;void dfs3 (int x,int f) siz[x] = 1 ,fat[x] = f,dep[x] = dep[f] + 1 ,son[x] = 0 ; for (int i = 0 ;i < G[x].size ();++i) { int y = G[x][i]; dfs3 (y,x); siz[x] += siz[y]; if (siz[y] > siz[son[x]]) { son[x] = y; } } } void dfs4 (int x,int f) if (son[f] == x) top[x] = top[f]; else top[x] = x; if (son[x]) dfs4 (son[x],x); for (int i = 0 ;i < G[x].size ();++i) { if (G[x][i] != son[x]) dfs4 (G[x][i],x); } } int LCA (int x,int y) while (top[x] != top[y]) { if (dep[top[x]] < dep[top[y]]) swap (x,y); x = fat[top[x]]; } return (dep[x] < dep[y]) ? x : y; } signed main () cin >> n >> q; for (int i = 1 ;i < n;++i) { int x;cin >> x;G[x].push_back (i+1 ); deg[x]++; if (x == 1 ) lis.push_back (i+1 ); } for (int i = 1 ;i <= n;++i) { if (!deg[i]) leaf[i] = 1 ; } for (int i = 0 ;i < lis.size ();++i) { dfs2 (lis[i],lis[i]); } dfs1 (1 ),dfs3 (1 ,0 ),dfs4 (1 ,0 ); int now = 0 ,las; while (q--) { char opt;int x; cin >> opt >> x; if (opt == '+' ) { ++now;las = 0 ; if (s[bel[x]].size ()) { int laslca = LCA (rk[*s[bel[x]].begin ()],rk[*s[bel[x]].rbegin ()]); las = rul[laslca]; } s[bel[x]].insert (dfn[x]); int lca = LCA (rk[*s[bel[x]].begin ()],rk[*s[bel[x]].rbegin ()]); if (!vis[bel[x]]) ++ans1; ++vis[bel[x]]; ans2 += rul[lca] - las; } else { --now;las = 0 ; int lca = LCA (rk[*s[bel[x]].begin ()],rk[*s[bel[x]].rbegin ()]); s[bel[x]].erase (dfn[x]); --vis[bel[x]]; if (!vis[bel[x]]) --ans1; if (s[bel[x]].size ()) { int laslca = LCA (rk[*s[bel[x]].begin ()],rk[*s[bel[x]].rbegin ()]); las = rul[laslca]; } ans2 -= rul[lca] - las; } printf ("%d %d\n" ,ans1,ans2-now); } return 0 ; }
K.King’s Heir
在国王去世的那一天,国王会让年龄最小但已满十八周岁的儿子继承国王,求哪一个儿子继承了国王,若没有儿子满足条件,则输出-1。保证国王不会有双胞胎。
$n \leq 100$
签到题,场上看到number第一反应就是有几个人导致挂了两发
直接扫一遍,这里用了一个比较巧妙的处理方法,注意到每个人的出生日期实际上是可以转化为 yyyy/mm/dd 的形式,我们可以用一个类似 hash 的办法把每个日期都化成一个整数,先判断是否满足条件,满足条件直接取最大值(出生日期最晚年龄最小)即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 int n;int a[N],b[N],c[N],x,y,z,ans,tmp;signed main () read (x,y,z,n); for (int i = 1 ;i <= n;++i) { read (a[i],b[i],c[i]); if (z - c[i] > 18 ) { int now = c[i] * 10000 + b[i] * 100 + a[i]; if (now > tmp) { tmp = now,ans = i; } } else if (z - c[i] == 18 ) { if (b[i] < y) { int now = c[i] * 10000 + b[i] * 100 + a[i]; if (now > tmp) { tmp = now,ans = i; } } else if (b[i] == y) { if (a[i] <= x) { int now = c[i] * 10000 + b[i] * 100 + a[i]; if (now > tmp) { tmp = now,ans = i; } } } } } if (ans) cout << ans; else cout << -1 ; return 0 ; }