Swin Transformer 学习笔记

学长推荐（2/20）

Motivation

随着 Transformer 在语言领域大杀四方，大家的研究目光也自然从 CNNs 转移到 Transformer 是否能在图像领域再下一城。对于 Transformer 来说，基本的单位是 Token，那么 Transformer 直接应用到高分辨率图像中，attention机制计算的复杂度和尺寸成平方关系，导致计算难以进行。所以就有了 Swin Transformer。

Main approach

Swin-Transformer 的架构是：把特征图变成层次化，并且具有和图像成线性关系的计算复杂度。从较小的图像块开始，在更深的 Transformer 层中逐步合并相邻图像块构建表示，计算复杂度在于，在一个窗口内局部计算 self - attention。而因为窗口内的图像块数量固定，所以复杂度和尺寸成线性关系。

Shifted Window based Self-Attention

这个是本篇最关键的 Module，标准的 Transformer 架构会通过 global self-attention 来计算 tokens 之间的关系，导致时间复杂度和尺寸成平方关系。本篇提出以局部窗口内计算 self-attention，也就是窗口以不重叠的方式均匀划分图像。假设每个窗口包含 $M\times M$ 个图像块，在 $h\times w$ 个图像块的图像上计算，全局的多头自注意力复杂度为 $\Omega(MSA) = 4hwC^2 + 2(hw)^2C$，而基于窗口的为 $\Omega(W-MSA) = 4hwC^2 + 2M^2hwC$ 。后者则是一个线性关系，一般我们取 $M = 7$。

Shifted window partitioning in successive blocks

这也提出了一个新问题，按照窗口划分实际上跨窗口的信息就没了。所以论文提出了移位窗口划分方法：在连续的 Swin Transformer 块之间交替使用两种划分配置。

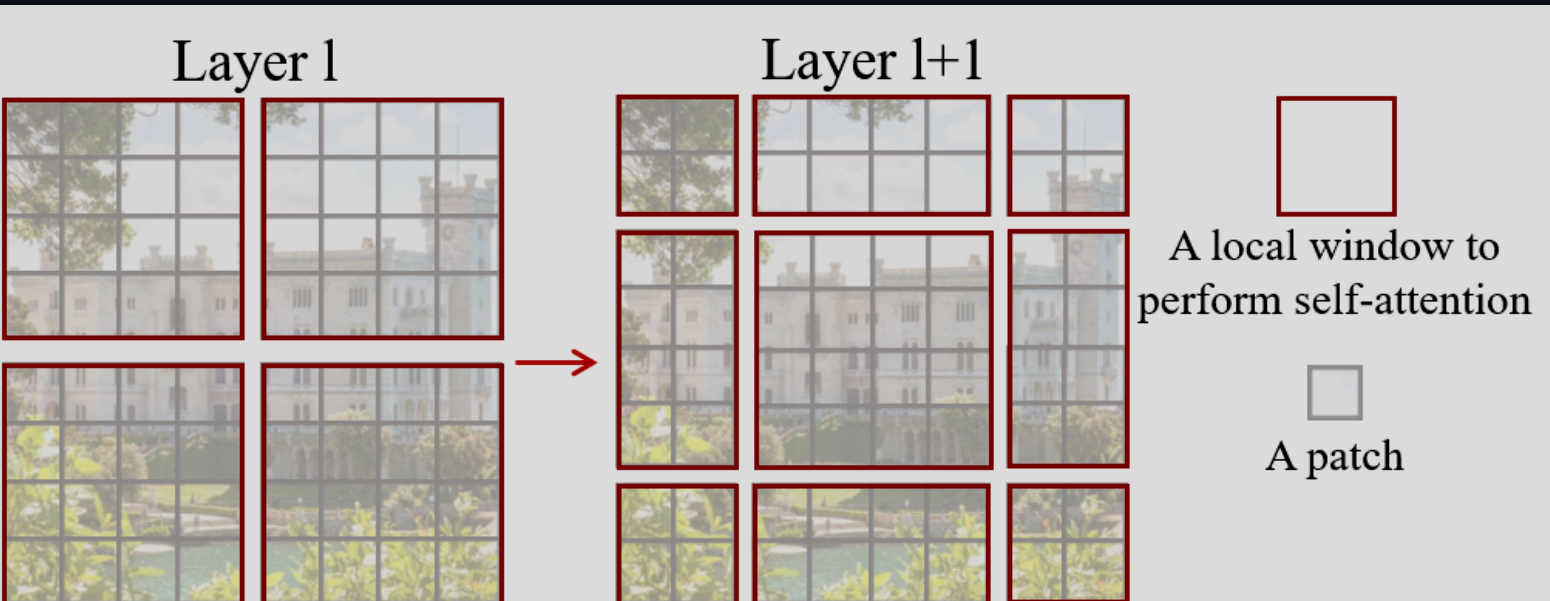
第一种就是常规的划分，第二种则是把整体的窗口位置移动了 $(\lfloor \frac{M}{2}\rfloor ,\lfloor \frac{M}{2} \rfloor)$ 个像素。并且连续的 Swin Transformer 块就这么计算：
$$
\hat{z}^l = \text{W-MSA}(\text{LN}(z^{l-1})) + z^{l-1}\
z^l = \text{MLP}(\text{LN}(\hat{z}^l)) + \hat{z}^l
$$
先对第一种常规的窗口化多头自注意力进行计算，并且加上残差链接。
$$
\hat{z}^{l+1} = \text{SW-MSA}(\text{LN}(z^l)) + z^l \
z^{l+1} = \text{MLP}(\text{LN}(\hat{z}^{l+1})) + \hat{z}^{l+1}
$$
和上一步差不多，重点在于选用了移动窗口的自注意力，实现了跨窗口的信息流动。

Efficient batch computation for shifted configuration

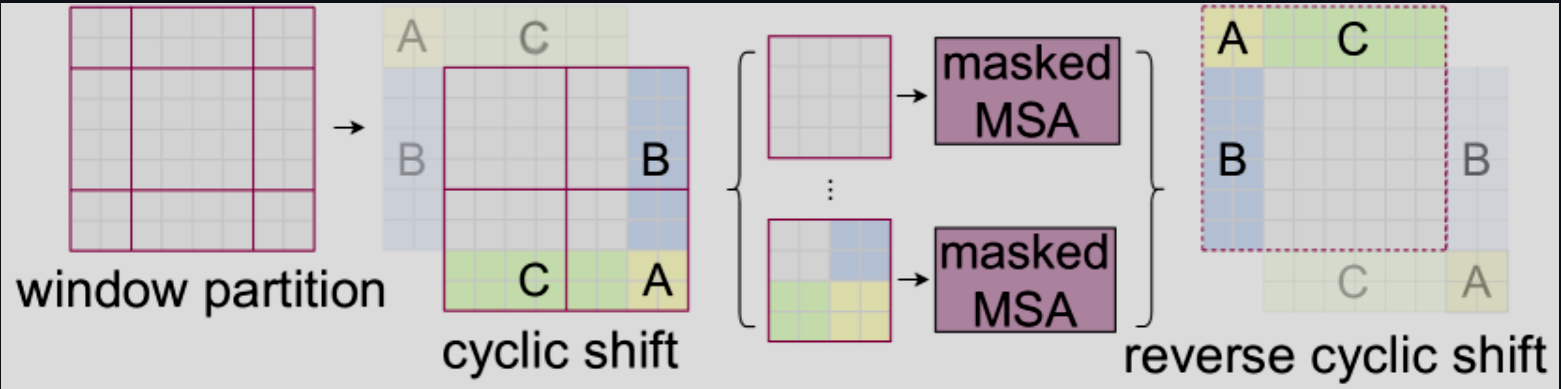
由于两种方法的交替使用会让窗口数量从 $\lceil \frac{h}{M} \rceil \times \lceil \frac{w}{M} \rceil$ 变成 $(\lceil \frac{h}{M} \rceil + 1) \times (\lceil \frac{w}{M} \rceil + 1)$,所以数量其实会多不少。所以论文采用循环移位的方法进行窗口计算，并且引入了掩码机制以防止重复计算。这也是本篇在工程技巧上选用的最有意思的一点：